Projects

Distance-to-Set Priors

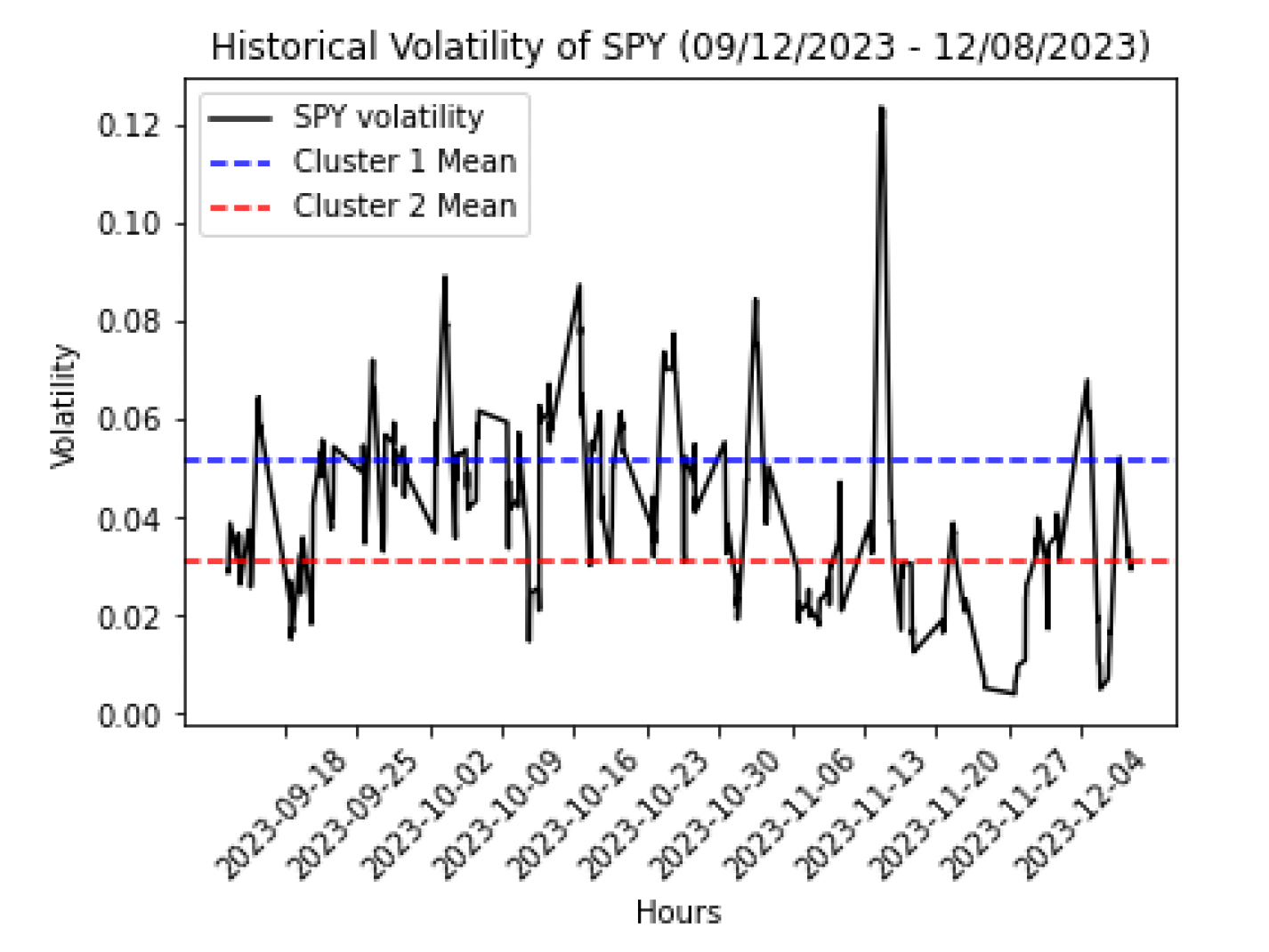
Modern Bayesian computation focuses on how to efficiently sample from posterior distributions, which combine observed data with prior beliefs. State-of-the-art samplers, like Hamiltonian Monte Carlo (HMC), are often referred to as gradient-based samplers as they use the geometry of the posterior to more efficiently sample from these posteriors. However, in addition to encoding data and prior beliefs, Bayesian models often encounter additional constraints (or side information) on their parameters. Not only do these constraints often make the posterior distribution intractible, they inherently complicate sampling from the target distribution because sample draws now need to satisfy constraints. Moreover, gradient-based samplers like HMC don’t always work well in the presence of constraints. In Distance-to-Set Priors and Bayesian Constraint Relaxation (Presman and Xu, AISTATS 2023), we propose a novel method to relax constraints by regularizing by the (squared) distance a point is from the constraint set. In additition to make the constraints approximately compatible with HMC, we show theoretical favorable properties for these samplers and improved sampling performance. In the picture below, for example, the competing approach (left) fails to sample from a distribution constrained to the sphere, while our approach (right) samples from the desired distribution.

More recently, we have proposed extensions of this approach in a certain class of non-Euclidean problems, known as divergence-to-set priors (Presman and Xu, JSM 2024), greatly expanding the types of settings where our methods can be applied.

Volatility Trading with Multi-Regime, Latent Factor Models

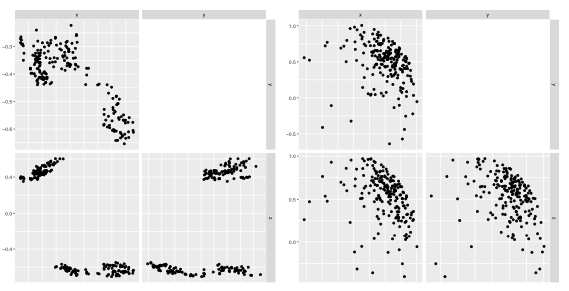
Volatility time series data exhibit many interesting phenonemon. In addition to intraday seasonality, volatility has been observed to cluster in multiple regimes (see example figure below). These phenomena make such data an interesting source for pattern recognition. As part of a class I took on Algorithmic Trading, I collaborated on team of PhD students to develop an equity-based volability trading strategy that combined ideas from elements from nonlinear time-frequency analysis and multi-regime, latent factor models to develop a strategy that identified trading signals based on changing volatility environments. We considered risk management actions, implemented our strategy in the Python-based backtesting platform QuantConnect, and identified strengths and risks of our strategy. Our full report can be found here.